7 Kryptografie

RNDr. Miroslav Šedivý

Kryptografie (volně přeloženo to znamená nauka o skrytém písmu) se v dnešním pojetí zabývá konstrukcí kryptografických algoritmů a schémat a určováním jejich vlastností. Naproti tomu kryptoanalýza se zabývá analýzou kryptografických algoritmů z hlediska jejich zranitelnosti a rovněž praktickým využitím získaných výsledků (například luštěním zašifrovaných zpráv bez znalosti odpovídajícího klíče). Oba obory se někdy nazývají společně kryptologií.

Sama kryptografie je dnes obor velice rozlehlý a vysvětlit alespoň základy na několika stranách je nelehký úkol, který se neobejde bez určitých zjednodušení. Proto jsou některá fakta uváděná v tomto doplňku podána zkrácenou formou, vyhýbáme se rovněž detailům, které vyžadují hlubší znalosti z matematiky. Případné zájemce o studium tohoto nesporně zajímavého oboru nezbývá než odkázat na příslušnou literaturu ([1] či [2], druhá jmenovaná je dokonce volně přístupná na Internetu).

Nedlouho poté, co lidstvo začalo pro uchovávání, případně přenášení nejrůznějších informací používat písmo, se objevily i snahy přenášet tyto informace takovým způsobem, aby byly přístupné jen určenému okruhu osob. Používaly se nejrůznější způsoby skrývání informací jako duté hole, neviditelné písmo a podobně (jako perlička vypadá způsob, používaný v dávnověku, kdy se poslům zpráva napsala na kůži lebky a poté, co vlasy dorostly, mohli vyrazit na cestu. Příjemci stačilo poslovi šetrným způsobem oholit lebku). Později se začaly používat systémy, které sice přítomnost zprávy přímo neskrývaly, ale utajovaly vlastní informaci – začaly se používat kódy a později šifry. Poslední dva pojmy se v praxi dost často nesprávně zaměňují, proto začneme definicí některých pojmů, což nám umožní se přesněji vyjadřovat při dalším výkladu.

Jako první si uvedeme definicí abecedy. Abecedou (označme ji A) rozumíme jakoukoliv konečnou množinu symbolů 

A = {a₁, a₂, … , a_n}

Prvkům této množiny říkáme písmena. Abecedu může představovat např. mezinárodní abeceda, česká abeceda, znaky z tabulky ASCII, čísla atd. Slovem nazýváme jakoukoliv konečnou posloupnost písmen z množiny A. Nechť S je nějaká podmnožina množiny všech možných slov, nazveme ji prostorem zpráv a budeme ji značit S(A). Jednotlivé prvky z S(A) nazveme zprávami.

Mějme nyní dvě abecedy, A a B a odpovídající prostory zpráv S(A) a S(B). Kódem nazýváme vzájemně jednoznačné zobrazení F z S(A) do S(B)

F : S(A) -> S(B)

tedy takové, že různé zprávy z S(A) se zobrazí na různé zprávy z S(B). Jestliže se zpráva M_A zobrazí na M_B, píšeme

M_B = F(M_A)

a říkáme, že zpráva M_B vznikla zakódováním zprávy M_A. Naopak ze zprávy M_B můžeme zprávu M_A získat procesem zvaným dekódování

M_A = F^-1(M_B)

kde F^-1 je inverzní zobrazení k F.

Z definice kódu (z jeho vzájemné jednoznačnosti) vyplývá, že jednou zakódovanou zprávu lze jednoznačně dekódovat, tedy ze znalosti M_B lze určit jednoznačně M_A, takže uvedená poslední rovnice má smysl. V praxi zpravidla bývá zobrazení F i F^-1 veřejně známé (jako např. v případě ASCCI kódu), takže není problém zprávy jak kódovat tak i dekódovat, i když jsou i výjimky (např. dříve ve vojenském či diplomatickém prostředí), kdy tento předpis je utajovaný (tajné kódy) a zprávy v S(B) jsou zvoleny tak, aby nenesly žádnou užitečnou informaci o svých protějšcích z S(A) (např. náhodné posloupnosti písmen z B).

Tajné kódy dříve používané ovšem měly tu nevýhodu, že jestliže byl předpis pro kódování prozrazen, musel být vyměněn, což nemusela být jednoduchá záležitost (klasický tajný kód představoval knihu o několika desítkách až stovkách stran, kde byly kódové výrazy nejen pro jednotlivé znaky, ale i pro složeniny dvou či tří znaků a popřípadě i celá slova či krátké věty[1]).

Šifra se od kódu liší tím, že samo zobrazení F je závislé na určitém parametru K (nazýváme jej klíč), takže nemáme jen jedno, ale celou množinu takových zobrazení.

F_K : S(A) -> S(B)

Jestliže se zpráva M_A s pomocí klíče K zobrazí (zašifruje) na M_B, píšeme

M_B = F_K(M_A)

opačný postup (dešifrování zprávy M_B ) lze napsat jako

M_A = F_K^-1(M_A)

Totéž pak můžeme zapsat také jiným způsobem:

šifrování

M_B = E (K , M_A)

a dešifrování

M_A = D (K´ , M_B)

kde D je zobrazení „opačné“ k  E a klíč K´ je s  K  určitým způsobem svázán. Z posledního zápisu pro dešifrování vidíme, že původní zpráva M_A je vlastně funkcí šifrované zprávy M_B a klíče K´ a bez znalosti K´ se tedy při dešifrování neobejdeme (to samozřejmě platí v případě, že šifrovací algoritmus je „správně“ postaven). Je samozřejmě možné vyzkoušet všechny potenciální klíče, to ale nemusí být jednoduché, pokud se klíč volí z dostatečně velké množiny přípustných hodnot. Zde je právě podstatný rozdíl mezi kódem a šifrou – samotné funkce E a D mohou být známy, to, co je potřeba obecně utajovat, jsou klíče.

Jestliže můžeme z hodnoty klíče K efektivně určit hodnotu klíče K´ a naopak (zde i dále pojem efektivně znamená dostupnými prostředky v přijatelném časovém úseku), hovoříme o symetrické šifře - v takovém případě můžeme poslední rovnici psát ve tvaru

M_A = D´ (K , M_B)

V dalším textu budeme psát pro zjednodušení jen D místo D´.

Pokud postavení K a K´ není symetrické (tedy znalost např. K  nám neumožňuje efektivně určit K´  ), mluvíme o šifře asymetrické. Následující schémata znázorňují procesy šifrování a dešifrování v obou uvedených případech

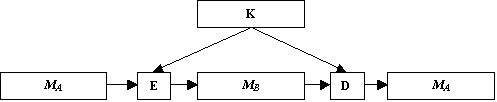
Obr. 7-1 Proces šifrování a dešifrování v případě symetrické šifry

Obr. 7-2 Proces šifrování a dešifrování v případě asymetrické šifry

Z porovnání obou schémat vyplývá důvod použití označení symetrická a asymetrická šifra.

7.1 Základní historické systémy

Dříve než se budeme zabývat moderními druhy kryptografických algoritmů, povězme si něco o základních dvou systémech, které stojí v základech většiny moderních algoritmů. Jde o substituční a transpoziční systémy. Dále budeme občas používat pojem otevřený text (zkratka OT), což je zpráva z S(A), a pojem šifrový text (zkratka ŠT), což je zpráva z S(B).

Substituční systém je takový systém, kdy pro daný klíč je každému písmenu vstupní abecedy vzájemně jednoznačně přiřazeno určité písmeno výstupní abecedy. Šifrování pak spočívá v tom, že otevřený text rozdělíme na jednotlivá písmena, najdeme jejich ekvivalenty ve výstupní abecedě a původní písmena jimi nahradíme (provedeme substituci – nahrazení). Výsledkem je šifrový text. Dešifrování probíhá obdobně. Ačkoliv je možných klíčů např. pro mezinárodní abecedu 26! ( » 4*10²⁶ ), tedy poměrně hodně, jedná se o kryptograficky slabý systém, který lze poměrně snadno luštit.

Klíč (posunutá abeceda):

A

B

C

D

E

F

G

…

…

T

U

V

W

X

Y

Z

C

D

E

F

G

H

I

…

…

V

W

X

Y

Z

A

B

Otevřený text

Z

P

R

A

V

A

P

R

I

J

A

T

A

Šifrový text

B

R

T

C

X

C

R

T

K

L

C

V

C

Obr. 7-3 Příklad substituce

Transpoziční systém funguje jinak. V tomto případě používáme stejné abecedy, slova mají délku rovnou délce tzv. transpozičního klíče (permutace), podle nějž přehážeme písmena v každém bloku. Je-li např. transpoziční klíč roven (3,6,1,2,4,7,5), znamená to, že ve výstupním bloku je jako první uvedeno třetí písmeno původního bloku, jako druhé je šesté písmeno bloku atd. Jestliže daný blok napíšeme jako (a₁ a₂ a₃ a₄ a₅ a₆), výsledkem bude blok (a₃ a₆ a₁ a₂ a₄ a₇ a₅). Tuto operaci provedeme s každým blokem. Opět se nejedná o bezpečný systém, dokonce ani při delším klíči (byť možností je opět hodně, n!, kde n je délka klíče). Varianta, kterou jsme uvedli, je tzv. horizontální transpozice, existují i jiné, my se jimi však zabývat nebudeme.

Klíč:

3

6

1

2

4

7

5

3

6

1

2

4

7

5

Otevřený text

Z

P

R

A

V

A

P

R

I

J

A

T

A

X

Šifrový text

R

A

Z

P

A

P

V

J

A

R

I

A

X

T

Obr. 7-4 Příklad transpozice

7.2 Symetrické šifry

Nejznámějším představitelem symetrických algoritmů je DES (Data Encryption Standard), který vznikl v roce 1976 jako odpověď na potřebu standardu v této oblasti. Autorský tým pocházel z IBM, nepochybný vliv na vývoj však měla i NSA[2]. DES je zároveň typickým představitelem tzv. blokových šifer a proto si na jejím příkladu ukážeme, jak většina blokových šifer funguje. Blokové šifry se vyznačují tím, že délka slova (nazýváme jej blok), se kterým pracují, je pevným násobkem délky písmen základní abecedy. Např. délka bloku DES je rovna 8 bajtům (tedy 64 bitů). Zpravidla pak sám algoritmus probíhá v několika opakujících se postupných krocích, nazývaných kolo nebo v kryptografickém žargonu také runda (z angl. round). Pro každé takové kolo se použije zpravidla tzv. pracovní klíč, který je odvozen ze základního klíče K.

Jak tedy DES pracuje? Odpověď nám dá následující obrázek, který schematicky popisuje jedno kolo DES (jeho základem je tzv. Feistelovo schéma):

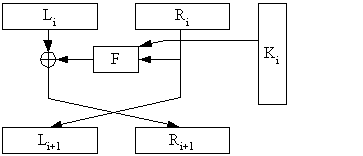
Obr. 7-5 Schéma jednoho kola DES

Základní blok o délce 64 bitů se rozdělí na dva bloky délky 32 bitů (L_i a R_i), blok R_i se okopíruje do následujícího levého bloku pro další kolo a zároveň slouží spolu s pracovním klíčem Ki jako vstupní hodnota pro tzv. transformační funkci F, její výstup se sečte (pomocí funkce XOR) s levým blokem a výsledek se umístí do pravého bloku pro další kolo. Tento postup se v případě DES aplikuje celkem 16 krát. Před vstupem do prvního kola se ještě provede určitá (pevná) transpozice celého bloku 64 bitů, po posledním šestnáctém kole se provede transpozice opačná. Dešifrování probíhá podle podobného schématu, pouze pracovní klíče pro jednotlivá kola se berou v opačném pořadí (ponecháváme na čtenáři, aby si ověřil, že tomu tak skutečně je - jde o základní vlastnost Feistelova schématu).

V klasickém algoritmu DES byla délka klíče sice 64 bitů, použito však bylo vždy je 56 bitů, ostatní sloužily jako zabezpečení. Během 90-tých let 20. století se však takováto délka klíče ukazovala jako nedostatečná a rovněž okolo samotného algoritmu DES panovaly určité nejasnosti, a proto se objevily další algoritmy, které měly délku klíče větší a rovněž jejich stavba byla robustnější. Uveďme si např. algoritmy 3DES, IDEA, BLOWFISH a v neposlední řadě standard pro 21.století – AES, který byl navržen pod názvem Rijndael. Jde o časem prověřené algoritmy, které při správném používání jsou schopny zprávy zabezpečit velmi spolehlivě.

Poznamenejme ještě, že kromě blokových jsou i další představitelé symetrických šifer – tzv. proudové šifry. Ty na rozdíl od blokových pracují přímo se slovy, jejichž délka je rovna jednomu písmenu. Uplatňují se zejména ve znakově orientovaných přenosech informací.

7.3 Módy blokových šifer

Blokové šifry, o kterých jsme dosud mluvili, většinou nepracují s jedním blokem, ale se zprávami, které sestávají z více bloků. Ukážeme si, jak lze s pomocí uvedených algoritmů takové zprávy šifrovat. Způsobů je více – hovoříme o tzv. módech šifrování.

Nejjednodušším módem je tzv. elektronická kódová kniha (ECB – Electronic Code Book). Jak již název napovídá, půjde o moderní variantu kódu, ovšem ne tak docela, protože jak již víme, kódy nemají klíč. Způsob šifrování je jednoduchý – zprávu rozdělíme na bloky o délce odpovídající bloku samotného algoritmu a tyto bloky jednoduše zašifrujeme (viz obr. 7-6, E - šifrování, D - dešifrování). Každý blok se šifruje stejným klíčem.

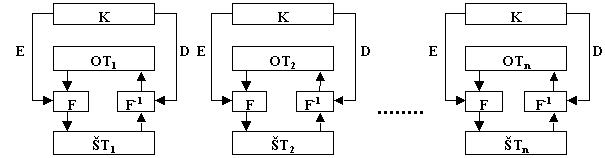
Obr. 7-6 Schéma šifrování a dešifrování v módu ECB

Výhodou je, že původní obsah jednoho bloku lze snadno změnit a znovu zašifrovat, aniž bychom museli opětovně šifrovat ostatní bloky zprávy (pokud používáme stále stejný klíč), to lze využít např. při šifrování obsahu pevného disku na úrovni sektorů. Nevýhodou takového postupu je to, že bloky mající stejný obsah se zašifrují stejně, takže je lze snadno odhalit. Tomu však je možné zabránit nejrůznějšími technikami. Např. ve zmíněném případě šifrování pevného disku můžeme ke klíči vždy přičíst pořadové číslo bloku, a tím máme pro bloky stejného otevřeného textu umístěné na různých místech různé šifrované bloky, i když původní obsah byl stejný.

Dalším v pořadí je mód se zpětnou vazbou šifrového textu (CFB – Cipher FeedBack). Schéma šifrování zprávy, kterou opět rozdělíme na jednotlivé bloky, je vidět na obr. 7-7. IV je náhodně generovaný blok nazývaný inicializační vektor, který zároveň bude tvořit nultý blok výsledného šifrového textu. Současně tento blok slouží jako vstupní hodnota pro funkci F, která provede vlastní blokové šifrování; výstupní hodnota této funkce se sečte (XOR) s příslušným blokem otevřeného textu - výsledkem je blok šifrového textu, který opět vstupuje do funkce F, atd. Tento mód má tu výhodu, že na rozdíl od ECB stejné bloky ve zprávě s vysokou pravděpodobností zašifruje různě a navíc má tzv. samosynchronizační vlastnost – pokud přijmeme jeden blok šifrového textu s chybou, tato se projeví pouze ve dvou blocích otevřeného textu. Má však i nevýhody – poslední blok je zašifrován jen pomocí operace XOR s výsledkem transformace předchozího bloku šifrového textu a lze tedy např. měnit jednotlivé bity tohoto bloku (změnou odpovídajícího bitu posledního bloku šifrového textu), aniž bychom změnili ostatní bity tohoto bloku (ověřte si to). V takovém případě, pokud můžeme předpokládat, co poslední blok otevřené zprávy přesně obsahuje, můžeme jeho obsah úspěšně změnit a podstrčit příjemci vlastní ukončení zprávy.

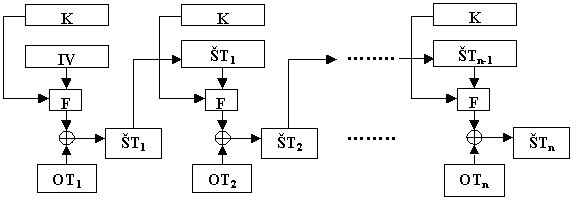
Obr. 7-7 Šifrování v módu CFB

Tuto nevýhodu odstraňuje poslední mód, o kterém se zmíníme, řetězový mód (CBC – CipherBlockChaining). Způsob šifrování je uveden na obr. 7-8. Stejně jako v případě CFB se generuje nejdříve IV, které je zároveň nultým blokem šifrového textu, a v každém kroku se předchozí šifrový text sčítá (XOR) s otevřeným textem, výsledek slouží jako vstupní hodnota pro funkci F, která provede vlastní blokové šifrování, a výstupní hodnotou je nový blok šifrového textu. Je vidět, že v tomto případě je i poslední blok „v bezpečí“.

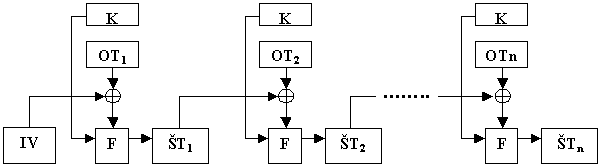
Obr. 7-8 Šifrování v módu CBC

Poslední dva módy se na rozdíl od ECB uplatňují spíše u přenosů zpráv, pokud se používají např. pro šifrování pevného disku, tak většinou jen na úrovni jednotlivých souborů.

7.4 Jednosměrné funkce – Hash

Dalšími algoritmy, které hrají v moderní kryptografii důležitou roli, jsou tzv. hash-algoritmy. Pokud se vrátíme k terminologii použité výše, jde o funkce z prostoru zpráv o velké mohutnosti do prostoru zpráv o pevně stanovené mohutnosti, které mají určité dané vlastnosti: budeme značit takovou funkci jako HASH

HASH : S(A) -> S(B)

a její hodnotu pro zprávu M jako H

H = HASH(M)

Základními požadavky na tyto funkce jsou jednosměrnost, tj. k dané hodnotě H nelze určit efektivně takovou hodnotu M, aby bylo

H = HASH(M)

a bezkoliznost, tj. nelze efektivně najít dvě různé zprávy M₁ a M₂ takové, aby platilo

HASH( M₁ ) = HASH( M₂ )

Dále (až dojde řeč na digitální podpis) uvidíme, že tyto vlastnosti hrají při použití hash-algoritmů zásadní roli.

Nejznámějšími představiteli hash-algoritmů jsou MD5 a SHA-1. MD5 je produktem firmy RSA Inc. (MD je zkratka od Message Digest) a její výstup (otisk zprávy) má velikost 128 bitů. Poněkud novější je SHA-1 (SHA je zkratka od Secure Hash Algorithm) s otiskem velikosti 160 bitů. V praxi se používají oba algoritmy (např. v zabezpečené elektronické poště), preferovaným se však v poslední době stává spíše SHA-1, z důvodu větší délky výstupu.

V obou případech je základem takzvaná jednosměrná funkce (funkce mající vlastnosti jednosměrnosti a bezkoliznosti, jak byly definovány výše) z prostoru zpráv o délce 128 nebo 160 bitů do prostoru zpráv o stejné mohutnosti - označme ji jako G. Vlastní zpráva je pak rozdělena na bloky m₁, m₂, …, m_n stejné délky (tedy 128 nebo 160 bitů) a je spočítána vlastní hodnota HASH podle níže naznačeného postupu (zde f je jednosměrná funkce, která má dva vstupy, IV je opět inicializační vektor - ten však v tomto případě bývá konstantní a konkrétní hodnoty závisí na použitém algoritmu, n je počet bloků zprávy)

H₀ = IV; H_i = f (H _i-1 , m_i ) i = 1, … , n ; HASH = H_n

Posledním výstupem ve schématu je vlastní HASH.

Na obdobné myšlence, jako hash - algoritmy, jsou založeny tzv. MAC-algoritmy (MAC - Message Authentication Code), které však používají klíč. Zatímco hodnotu HASH k dané zprávě může spočítat kdokoliv, MAC pouze se znalostí použitého klíče. MAC se proto používá k zabezpečení celistvosti zprávy (klíč samozřejmě zná jen odesilatel a příjemce).

7.5 Kryptografické systémy s veřejným klíčem

Blokové šifry mají jednu velkou výhodu – jsou poměrně rychlé, vzhledem k tomu, že pracují najednou s celým blokem znaků. Jak však z definice symetrické šifry plyne, mají i jednu nevýhodu – je potřebné utajovat klíč K. Jestliže si chceme takto s někým šifrovat, musíme mu klíč nejdříve bezpečným způsobem (tedy tak, aby jej nikdo jiný nemohl získat) předat, což nemusí být tak jednoduché.

Tento problém je možné vyřešit pomocí asymetrické šifry. Připomeňme, že v případě asymetrické šifry ze znalosti klíče K pro zašifrování nelze efektivně určit klíč K´ pro dešifrování, takže pokud bychom poskytli osobě, s níž chceme komunikovat, klíč K, může jej použít pro zašifrování zprávy určené pro nás, aniž by bylo nutné klíč K skrývat, protože dešifrování jsme schopni provést pouze my (jen my máme odpovídající klíč K´). Na tomto postupu jsou založeny právě systémy s veřejným klíčem.

V systémech s veřejným klíčem máme soukromý (privátní) klíč K_P a klíč veřejný K_V. Veřejný klíč určitým způsobem zveřejníme, privátní klíč ponecháme v tajnosti. Kdokoliv pak může použít veřejný klíč pro zašifrování zprávy určené pro nás a jen my budeme schopni zprávu dešifrovat.

Na čem jsou takové systémy založeny? Zpravidla to bývá na matematických postupech, které jsou v jednom směru jednoduché, v opačném směru složité. Jeden z nejjednodušších takových postupů nám poskytuje i matematika základní školy. Je určitě jednoduché spočítat součin dvou čísel, složité však je rozložit daný součin na prvočinitele (pokud daný součin je dostatečně velké číslo). Na tomto problému zvaném faktorizace přirozených čísel je postaven kryptografický systém s veřejným klíčem, který byl nalezen jako jeden z prvních – RSA.

RSA byl poprvé publikován v roce 1977 trojicí vědců R. Rivestem, A. Shamirem a L. Adlemanem (podle počátečních písmen autorů je systém nazýván) a jeho myšlenka je následující: mějme dvě dostatečně velká prvočísla p a q. Jejich součin označme N, tedy N = p * q. Dále najdeme dvě taková čísla e a d, aby jejich součin dával zbytek 1 při dělení číslem j = (p ‑ 1)*(q ‑ 1), tedy

e * d = k * j + 1.

Připomeňme, že pro číslo j platí tzv. Eulerova věta, tj. pro a nesoudělné s N je

a ^j = 1 mod N

Vezmeme-li nyní číslo M, které je menší než N a nemá s ním společného dělitele, tedy není dělitelné p nebo q, a umocníme ho na exponent e, po vydělení výsledku číslem N dostaneme zbytek, který označíme C. Je tedy s použitím zápisu modulární aritmetiky

C = M ^e mod N

Tím jsme dostali šifrovanou zprávu (v případě, že zpráva je větší než N, rozdělí se na menší kousky). Umocníme-li tento vztah na exponent d, dostaneme

C ^d = ( M ^e) ^d mod N = M ^{e * d} mod N = M ^{k * j + 1} mod N = M ¹ mod N

(poslední rovnost vyplývá z Eulerovy věty), tedy máme vlastně

M = C ^d mod N

Stejný vztah se dá dokázat i pro námi vyloučené případy, kdy je M dělitelné p nebo q. Jestliže za veřejný klíč zvolíme čísla N a e, a ostatní utajíme, získáváme skutečný systém s veřejným klíčem: kdokoliv může jakoukoliv zprávu zašifrovat do tvaru C = M ^e mod N, jen my ale budeme moci spočítat M = C ^d mod N, neboť d známe jen my. Aby bylo možné zjistit d, je nutné znát právě rozklad čísla N, což, jak jsme uvedli, je velmi složitý problém. Pravda, mohli bychom také zprávu C „odmocnit“ pomocí e a tak získat původní zprávu, ale i to je prakticky nemožné.

To co jsme si uvedli, je samozřejmě jen základní myšlenka samotného systému, praktická realizace je trochu komplikovanější. Příkladem implementace je například standard PKCS #1 navržený firmou RSA Inc. Existují samozřejmě i jiné systémy, např. známý je systém ECC, založený na tzv. eliptických křivkách nebo systémy založené na tzv. diskrétním logaritmu (ElGamal, DSA).

Ale i systémy s veřejným klíčem mají nedostatky. Jedním z nich je např. pomalost výpočtů. Je třeba si uvědomit, že délka bloku zprávy je např. v případě RSA rovna 512 a více bitů, takže operace násobení a výpočtu zbytku (modulo N) probíhají relativně pomalu. Pokud bychom chtěli takto šifrovat zprávu o délce v násobcích MB, trvalo by to neúnosně dlouho.

Praktická realizace je proto poněkud jiná. Pro vlastní šifrování zprávy se volí některá ze symetrických šifer (jsou rychlé), dále se zvolí náhodný klíč (nazývá se zpravidla tajný klíč) a zpráva se zašifruje. Pomocí asymetrické šifry se pak přenese pouze zvolený tajný klíč (má mnohem menší – konstantní - délku než samotná zpráva) a zašifrovaná zpráva. Příjemce nejprve dešifruje tajný klíč a s jeho pomocí pak samotnou zprávu. Příkladem implementace je např. standard PKCS #7.

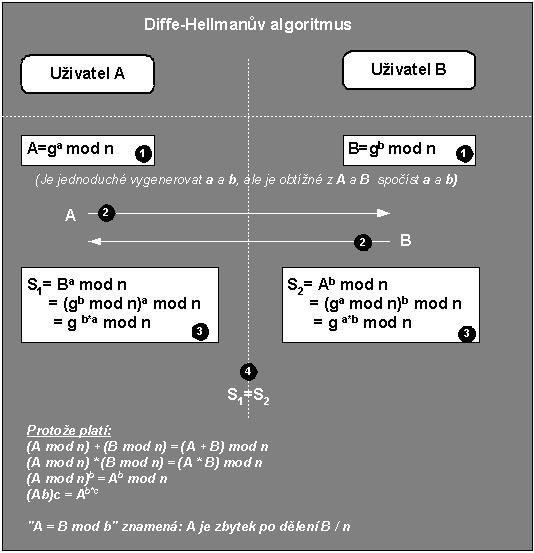
Obr. 7-9 Jiným asymetrickým algoritmem je Diffie-Hellmanův algoritmus: Uživatel A si s uživatelem B vymění veřejná Diffie-Hellmanova čísla A a B. Na základě těchto veřejných čísel si uživatelé spočtou „soukromá“ čísla S₁ a S₂, která jsou stejná a tak je lze využít např. jako symetrický šifrovací klíč.

7.6 Digitální podpis

Zatím jsme si vysvětlili, jak lze kombinaci symetrických a asymetrických algoritmů použít při šifrování zpráv. Asymetrické algoritmy však mají ještě jedno využití - umožňují nám tzv. podepisovat zprávy. Ukážeme si to na případu RSA.

Obecný postup je následující: Vezmeme zprávu M a spočteme její hash H. Poté vytvoříme novou zprávu S (můžeme ji nazvat podpis) pomocí privátního exponentu d

S = (H ) ^d mod N

Příjemci pošleme původní zprávu M a podpis S.

Dvojice M a S má následující vlastnosti

· z hodnoty S  lze získat hash původní zprávy M pomocí veřejného exponentu e

H = S ^e mod N

· je snadné ověřit, zda vlastní zpráva nebo podpis nebyly změněna během přenosu - ze zprávy M vypočtená hash ‑ hodnota

H = HASH (M)

by měla odpovídat hodnotě H vypočtené v předchozím kroku, takže by mělo platit

HASH (M) = S ^e mod N

· pokud víme, komu daný veřejný klíč patří, můžeme si být jisti, že zpráva je od něj (pokud ověření podpisu v předchozím kroku mělo kladný výsledek a samozřejmě pokud dotyčný uchoval svůj privátní klíč v utajení)

Uvedené vlastnosti jsou zaručeny jednosměrností hash algoritmu a asymetričností RSA. (Např. není možné „ukrást“ originální podepsanou zprávu s platným podpisem a vyměnit pouze vlastní zprávu, protože by nová zpráva musela mít stejnou hash - hodnotu jako původní zpráva a to nejsme schopni provést – brání tomu jednosměrnost hash-algoritmu.) Stejné závěry samozřejmě platí i v případech jiných systémů s veřejným klíčem (ECC, DSA, …).

Zbývá otázka, jakým způsobem zajistit bezpečné zveřejnění našeho veřejného klíče. Tento problém lze vyřešit použitím certifikátů (viz kapitola PKI).

7.7 Kryptoanalýza

Kryptoanalýza se, jak už jsme se zmínili, zabývá analýzou slabin jednotlivých algoritmů a jejich implementací, a to s dvěma odlišnými cíli, podle toho, kdo se jí zabývá. Buď s cílem vylepšit vlastní algoritmy nebo s cílem luštit cizí zprávy (případně se podepisovat za někoho jiného atd.). Snad nejznámějším případem úspěšné kryptoanalýzy je činnost britských analytiků za 2.světové války, kteří úspěšně luštili zprávy šifrované pomocí německého stroje Enigma. Hodně dlouhou dobu se kryptoanalýzou zabývaly hlavně vojenské a kontrašpionážní složky už jen z toho důvodu, že mimo tyto oblasti se šifrování zpravidla nepoužívalo.

Po nástupu elektronizace komerce se však situace změnila, kryptografie a s ní i kryptoanalýza se staly veřejnými vědami a věčný „boj“ mezi kryptografy a kryptoanalytiky se tak přenesl i do civilní, resp. komerční sféry. Dokladem toho jsou nejrůznější mezinárodní konference kryptologů. V roce 1999 se jedna taková – Eurocrypt – konala v Praze.

Je to právě kryptoanalýza, která dává tvůrcům nových schémat do rukou nástroje pomáhající zlepšit vlastnosti jimi produkovaných algoritmů. Za všechny uveďme např. objevy lineární a později diferenční analýzy (převážně určené pro symetrické šifry) nebo objev metody síta číselného tělesa (předtím kvadratického), které výrazně posunuly hranice možností faktorizace čísel (používá např. RSA). Zároveň výsledky analýz nejrůznějších implementací ukazují, že dané (i velmi silné) algoritmy mohou velice ztratit na síle právě špatnou implementací. Opatrnost je tedy vždy na místě, ať už se jedná o tvorbu aplikací nebo jejich používání.

Literatura:

[1] Schneier, Bruce : „Applied Cryptography“, John Wiley & Sons 1996

[2] Meneyes a. J., Oorschot, P. C., Vanstone S.A. : „Handbook of Applied Cryptography“, CRC Press 1997

---

[1] Je to možná překvapující, ale poslední tajné kódy se používaly ještě i v druhé polovině dvacátého století.

[2] NSA (National Security Agency – Národní bezpečnostní agentura) – je agentura vlády USA, která má mj. na starosti výzkum a vývoj v oblasti kryptografie a kryptoanalýzy, zabývá se i praktickým luštěním šifrovaných zpráv, které zachytí. Její činnost je přísně utajována.