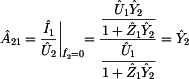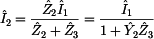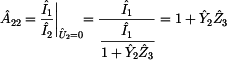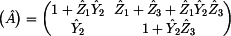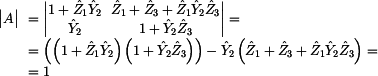

Komplexní čísla
Motivace
Pro numerické i obecné řešení elektrických obvodů
napájených harmonickým napětím je nezbytná znalost základních operací s
komplexními čísly. Toto cvičení dává studentům možnost ověřit si, zda znají
základní operace s komplexními čísly nutné pro úspěšné řešení elekrických
obvodů.
Probírají se tato témata:
Základní tvary a jejich
význam
Převod mezi nimi
Jako příklady se počítají:
převod z
exponenciálního na složkový tvar
převod ze složkového tvaru na exponenciální
Základní tvary
Základní tvary komplexních čísel Komplexní čísla jsou ve
čtyřech tvarech:
- geometrický
- složkový
- trigonometrický
- exponenciální
Při řešení elekrických obvodů se používají dva
tvary:
- složkový, nutný ke sčítání a odečítání, méně vhodný pro násobení a dělení,
nevhodný pro odmocňování, umocňování apod.
- exponenciální vhodný k násobení, dělení, umocňování, odmocňování, nelze
použít ke sčítání a odečítání
Ve složkovém tvaru píšeme komplexní
číslo takto
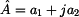
kde
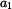
je reálná a
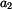
imaginární
složka,
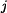
je imaginární jednotka s touto vyjímečnou vlastností
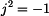
Pro
exponenciální tvar platí vztah
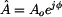
kde
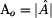
je
absolutní hodnota nebo modul a
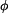
je úhel, který s osou X
svírá přímka směřující z počátku do komplexního čísla, viz část Geometrické
znázornění komplexních čísel. V analytické geometrii se jedná o průvodič bodu. V
teorii obvodů budeme však často mluvit o amplitudě
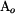
a fázovém úhlu, či
jednoduše jen fázi
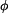
.
Geometrické znázornění komplexních čísel
Ke snadnějšímu pochopení dvou základních tvarů komplexního čísla,
složkového a exponenciálního, by měl sloužit tento obrázek
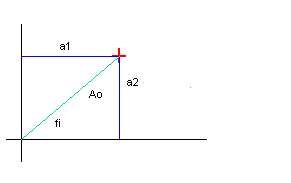
Komplexní číslo můžeme chápat jako bod v rovině. Reálná
složka
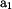
a imaginární složka
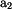
jsou jeho kartézskými souřadnicemi, zatímco amplituda
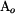
a fáze
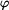
souřadnicemi polárními, po řadě průvodič a úhel.
Z tohoto obrázku lze
snadno odvodit převodní vztahy
Převod složkového tvaru na
exponenciálníPoužijeme Pytagorovu větu a definice funkce tangens.
Pozor vztah pro fázi platí jen v pravé polorovině.
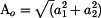
......
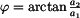 Převod exponenciálního tvaru na složkový
Převod exponenciálního tvaru na složkový Použijeme definice
funkcí sinus a kosinus
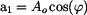
......
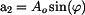
Převod mezi základními tvary
Chceme-li převodní vztahy pro zápis komplexního čísla čistě matematicky,
musíme použít goniometrického tvaru a jeho vztah ke tvaru složkovému a
exponenciálnímu
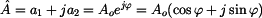 Převod exponenciálního tvaru na složkový
Převod exponenciálního tvaru na složkový
V předchozí rovnici zjednodušíme tím, že vynecháme některé části
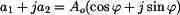
Z podmínky, že reálné a imaginární části na obou stranách
rovnixce se musí rovnat, dostaneme hledané vztahy
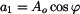
.....
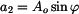 Převod
složkového tvaru na exponenciální
Převod
složkového tvaru na exponenciálníPředchozí vztahy umocníme, sečteme a
odmocníme. Získáme vztah pro amplitudu.
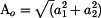
Vytvoříme podíl
vztahů pro složky a z něho dostaneme vztah pro fázi
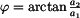
Tento vztah však
platí jen pro nezápornou reálnou složku,
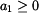
, tj. pro fázový úhel v
rozsahu
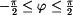
. Pokud je reálná složka záporná,
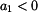
, je fázový úhel v
dalších dvou kvadrantech. V tomto případě je nutno použít vztahů

pro
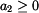

pro
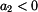
Příklady
Převod z exponenciálního tvaru na složkový
Převod ze složkového tvaru na exponenciální
Matematické základy teorie obvodů
Matematické základy teorie obvodů: (PDF-dokument)

Matematické základy teorie obvodů
Komplexní čísla
Komplexní čísla (soubor PDF):

Komplexní
čísla
Elementární komplexní funkce
Elementární komplexní funkce (PDF dokument):

Elementární komplexní funkce
Střídavé proudy
Střídavé proudy (PDF dokument):

Střídavé
proudy
Základní prvky
Základní prvky (PDF dokument):

Základní
prvky
Stejnosměrné buzení
Stejnosměrné buzení (PDF dokument):

Stejnosměrné buzení
Harmonické buzení
Harmonické buzení (PDF dokument):

Harmonické buzení
Náhradní obvody
Náhradní obvody (PDF dokument):

Náhradní
obvody
Přechodový jev
Přechodový jev (PDF dokument):

Přechodový jev
Přechodový jev - obrázky
(DOC)

Přechodový jev - Obrázky
Trojfázové obvody
Trojfázové obvody (PDF dokument):

Trojfázové obvody
Dvoubrany - Příklady
Dvoubrany - Příklady (PDF dokument):

Dvoubrany
- Příklady
Nelineární prvky
Dvoubrany - Příklady (PDF dokument):

Nelineární prvky
Dvoubrany
Kaskádní matice
Základní vztahy
Kaskádní rovnice dvojbranu získáme, zvolíme-li jako nezávisle
proměnné výstupní veličiny dvojbranu, tedy výstupní napětí a proud
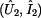
. Závislými
proměnnými jsou pak proměnné
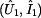
.
Použití nalézají především při posuzování přenosu signálu ze vstupu dvojbranu
na jeho výstup, který je zakončen pasivním dvojpólem nebo vstupem dalšího
dvojbranu. Právě proto zde volíme opačný smysl výstupního proudu než pro
obecnou charakteristiku dvojbranu.
Volba výstupního proudu pro je na následujícím obrázku:
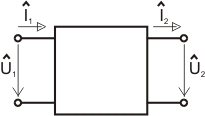 |
 |
| Volba kladných smyslů pro kaskádní rovnice
dvojbranu |
Pro výstupní proud tekoucí zátěží mají kaskádní rovnice následující
tvar:
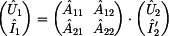
Rozepsáním těchto rovnic dostaneme soustavu dvou
rovnic o čtyřech parametrech
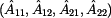
a se dvěma nezávislými veličinami
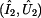
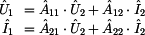
Význam těchto prvků a jejich rozměry vyplývají ze stavů
naprázdno a nakrátko po vyjádření z výše uvedených rovnic.
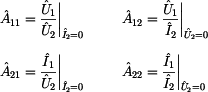
Kaskádním spojením dvojbranů rozumíme takové zapojení, kdy je k
výstupní bráně jednoho dvojbranu zapojena vstupní brána jiného dvojbranu, viz
následující obrázek.
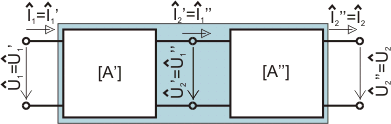 |
 |
| Kaskádní spojení
dvojbranů |
Takovéto spojení je zřejmě vždy
regulární. Je-li výstupní napětí a proud jednoho dvojbranu vstupním
napětím a proudem druhého dvojbranu, platí:
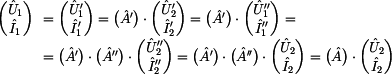 Kaskádní matice
Kaskádní matice výsledného dvojbranu se tedy
rovná:
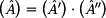
Jak vidíme, tak výsledná matice dvojbranu je
součinem matic dílčích dvojbranů. Tento poznatek lze aplikovat
na libovolné množství kaskádně spojených dvojbranů. Je však důležité vzít na
vědomí, že součin matic není komutativní (matematicky nemusí být často ani
možný), čili pořadí dvojbranů má na výsledek velmi zásadní vliv.
V následující části se budeme zabývat výpočtem těch nejjednodušších
dvojbranů, které později spojíme do kaskády a dokážeme si tím tak
platnost výše uvedeného vzorce, čili že výsledná matice kaskádně spojených
dvojbranů je rovna součinu matic dílčích dvojbranů.
Nyní přejděme k několika málo ukázkovým příkladům výpočtu těch
nejjednodušších dvojbranů:
První příklad si vysvětlíme podrobněji a v
dalších příkladech budeme již uvádět pouze změny způsobené jiným vnitřním
zapojením dvojbranu.
Řešené příklady
Příklad 1: Dvoubran typu I
| Příklad. |
Výpočet jednoduchého dvojbranu typu I:
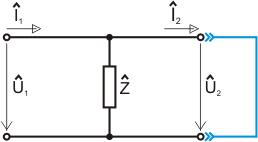
Mějme
dvojbran definovaný na následujícím obrázku:
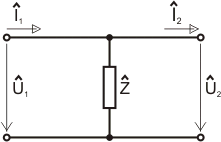
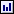
Nyní
přistoupíme k výpočtu prvků kaskádní matice A:
Prvek 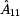 je
definován jako poměr vstupního napětí ku výstupnímu při zapojení
výstupních svorek dvojbranu naprázdno, tak jak ukazuje předchozí obrázek. je
definován jako poměr vstupního napětí ku výstupnímu při zapojení
výstupních svorek dvojbranu naprázdno, tak jak ukazuje předchozí obrázek.
Z obrázku je zřejmé, že výstupní napětí je rovno vstupnímu (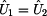 ),
čili prvek ),
čili prvek 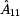 je roven: je roven:
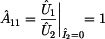
Prvek 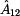 je
definovaný jako poměr vstupního napětí ku výstupnímu proudu při zapojení
výstupních svorek dvojbranu nakrátko, tak jak je znázorněno na předchozím
obrázku. je
definovaný jako poměr vstupního napětí ku výstupnímu proudu při zapojení
výstupních svorek dvojbranu nakrátko, tak jak je znázorněno na předchozím
obrázku.
Je zřejmé, že impedance 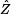 je zkratována a
nemá tedy v obvodu žádný význam. Z toho můžeme odvodit, že platí je zkratována a
nemá tedy v obvodu žádný význam. Z toho můžeme odvodit, že platí 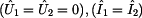 . Při
znalosti těchto poměrů lze již snadno vypočítat prvek . Při
znalosti těchto poměrů lze již snadno vypočítat prvek 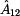 : :
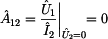
Jako poměr vstupního proudu ku výstupnímu
napětí při zapojení výstupních svorek dvojbranu naprázdno je definován
prvek 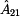 . K analýze použijeme tedy prvně uvedený obrázek z tohoto
příkladu. . K analýze použijeme tedy prvně uvedený obrázek z tohoto
příkladu.
V tomto příkladě opět platí rovnost vstupního a výstupního
napětí 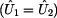 , viz obrázek. Vstupní proud dvojbranu , viz obrázek. Vstupní proud dvojbranu  snadno vyjádříme snadno vyjádříme
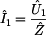 .
Nyní již známe vše co potřebujeme pro výpočet prvku .
Nyní již známe vše co potřebujeme pro výpočet prvku 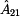
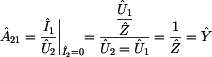
Prvek 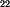 je definován jako
poměr vstupního ku výstupnímu proudu při zapojení výstupních svorek
dvojbranu nakrátko, viz. druhý obrázek tohoto příkladu. je definován jako
poměr vstupního ku výstupnímu proudu při zapojení výstupních svorek
dvojbranu nakrátko, viz. druhý obrázek tohoto příkladu.
Opět nejdříve
určíme známé veličiny. Platí zde rovnost vstupního a výstupního napětí
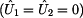 a i rovnost vstupního a výstupního proudu
a i rovnost vstupního a výstupního proudu 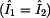 , neboť impedance , neboť impedance
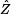 zde opět nemá žádný význam neboť je zapojením nakrátko zkratována. Znalost
těchto několika triviálních parametrů nám již umožňuje bez problémů
spočítat prvek
zde opět nemá žádný význam neboť je zapojením nakrátko zkratována. Znalost
těchto několika triviálních parametrů nám již umožňuje bez problémů
spočítat prvek 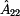
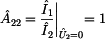
Tímto jsme spočetli všechny prvky kaskádní
matice (A). Ta má tedy ve výsledku tvar:
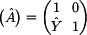
Porovnáním prvků 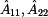 si snadno oběříme
souměrnost dvojbranu. Jelikož v našem případě platí si snadno oběříme
souměrnost dvojbranu. Jelikož v našem případě platí 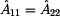 ,
můžeme řící, že dvojbran je podélně souměrný. ,
můžeme řící, že dvojbran je podélně souměrný.
Vypočítáním
determinantu kaskádní matice |A| si ověříme reciprocitu
dvojbranu. Ten je reciprocitní, pokud je determinant
kaskádní matice roven jedné.
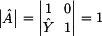
Tímto jsme si dokázali reciprocitu
dvojbranu. |
Příklad 2: Dvoubran typu "pomlčka"
Nyní si ukážeme výpočet dalšího triviálního dvojbranu, kde je impedance
zapojena do podélné větve, narozdíl od předchozího příkladu, kde byla zapojena
"mezi" svorkami dvojbranu.
| Příklad. |
Výpočet jednoduchého dvojbranu typu "pomlčka":
Nechť máme dvojbran uvedený na následujícím obrázku:
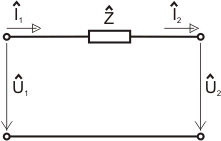
Ze zapojení
naprázdno, tak jak je uvedeno na obrázku, určíme analýzou obvodu potřebné
parametry. Vyjdeme opět z již dobře známého vzorce pro 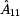 . .
Pro nulový
proud 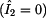 bude zřejmě nulový i proud bude zřejmě nulový i proud 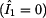 , neboť na
impedanci , neboť na
impedanci 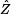 nemůže v tomto případě dojít k žádnému úbytku napětí. Z toho
vyplývá i rovnost obou napětí, vstupního a výstupního nemůže v tomto případě dojít k žádnému úbytku napětí. Z toho
vyplývá i rovnost obou napětí, vstupního a výstupního 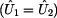 . Nyní již máme vše
potřebné pro vyjádření hodnoty prvku . Nyní již máme vše
potřebné pro vyjádření hodnoty prvku 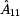 : :
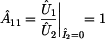
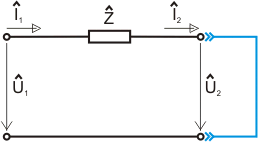
Prvek 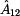 vychází ze zapojení výstupních svorek dvojbranu nakrátko, tak jak je
znázorněno na tomto obrázku a daného vzorce pro
vychází ze zapojení výstupních svorek dvojbranu nakrátko, tak jak je
znázorněno na tomto obrázku a daného vzorce pro 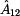
Z obrázku je
zřejmá rovnost obou proudů 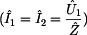 . Napětí tentokrát
vyjadřovat nemusíme, neboť si plně vystačíme s proudy. Dosazením
předchozích úvah do vzorce pro prvek . Napětí tentokrát
vyjadřovat nemusíme, neboť si plně vystačíme s proudy. Dosazením
předchozích úvah do vzorce pro prvek 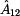 dostáváme: dostáváme:
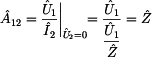
Další prvek 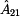 určíme ze zapojení
naprázdno, podle prvního obrázku tohoto příkladu a vzorce pro určíme ze zapojení
naprázdno, podle prvního obrázku tohoto příkladu a vzorce pro 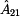 . .
V tomto případě opět platí rovnost obou proudů 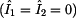 , neboť nedochází k
úbytku napětí na impedanci , neboť nedochází k
úbytku napětí na impedanci 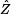 . Z tohoto závěru
plyne i rovnost obou napětí, vstupního a výstupního . Z tohoto závěru
plyne i rovnost obou napětí, vstupního a výstupního 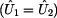 . Už z první
rovnosti jasně plyne výsledek prvku . Už z první
rovnosti jasně plyne výsledek prvku 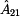 : :
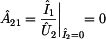
Poslední zbývající prvek 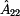 určíme opět ze
zapojení nakrátko výstupní brány dvojbranu podle druhého obrázku tohoto
příkladu a ze vzorce pro prvek určíme opět ze
zapojení nakrátko výstupní brány dvojbranu podle druhého obrázku tohoto
příkladu a ze vzorce pro prvek 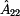 . .
V tomto
zapojení je opět zřejmá rovnost obou proudů 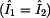 . Podíváme-li se
ale na vzorec pro tento prvek, zjistíme, že nemusíme tyto proudy ani
explicitně vyjadřovat, neboť se ve vzorci pokrátí. . Podíváme-li se
ale na vzorec pro tento prvek, zjistíme, že nemusíme tyto proudy ani
explicitně vyjadřovat, neboť se ve vzorci pokrátí.
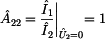
Máme tedy spočtenu celou kaskádní matici
(A), jež je ve výsledku rovna:
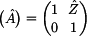
Opět z rovnosti prvků 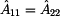 můžeme
konstatovat, že se jedná o podélně souměrný dvoubran. Výpočtem
determinantu kaskádní matice |A| si opět ověříme
reciprocitu dvoubranu. můžeme
konstatovat, že se jedná o podélně souměrný dvoubran. Výpočtem
determinantu kaskádní matice |A| si opět ověříme
reciprocitu dvoubranu.
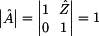
Z uvedené rovnosti jasně vyplývá, že se jedná o
reciprocitní dvoubran. |
Příklad 3: Dvoubran typu "velké otočené Gamma"
Nyní si ukážeme výpočet dalšího dvojbranu s pomocí kterého budeme nakonci
ověřovat správnost odvození vztahu pro
kaskádní matici dvojbranů
spojených do kaskády.
| Příklad. |
Výpočet jednoduchého dvojbranu typu "velké otočené
Gamma":
Poučení: Výpočty prvků matice (A)
nejsou v obecných případech tak triviální jako v předcházejích dvou
příkladech, neboť vstupní napětí a proudy nemusejí být rovny, či "snadno"
závislé na výstupních. Je proto důležité brát tyto poznatky při výpočtech
na zřetel.
Máme dvojbran definovaný zapojením na následujícím
obrázku:
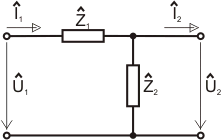
Podíváme-li se na
obrázek podrobněji, určitě každý pozná nezatížený odporový dělič,
čili nic nového.
Prvek 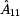 vyjádříme ze
zapojení naprázdno jak je znázorněno na prvním obrázku tohoto příkladu a
ze vztahu pro prvek vyjádříme ze
zapojení naprázdno jak je znázorněno na prvním obrázku tohoto příkladu a
ze vztahu pro prvek 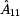 . .
Pro nezatížený dělič napětí platí známý vztah:
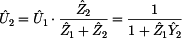
Dosazením uvedeného vztahu do vzorce pro prvek 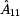 dostáváme:
dostáváme:
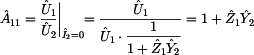
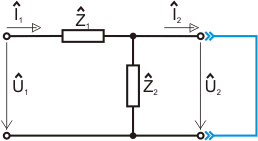
Výpočet dalšího
prvku 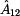 vychází ze zapojení nakrátko, jak je uvedeno na předcházejícím
obrázku tohoto příkladu a ze vzorce pro prvek vychází ze zapojení nakrátko, jak je uvedeno na předcházejícím
obrázku tohoto příkladu a ze vzorce pro prvek 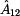 . .
Z obrázku lze
snadno poznat, že zde opět nastává rovnost obou proudů, vstupního a
výstupního, pro který platí 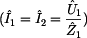 . .
Dosazením do
vzorce pro prvek 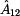 dostáváme: dostáváme:
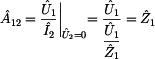
Výpočet prvku 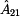 vychází ze
zapojení naprázdno, tak jak znázorňuje první obrázek tohoto příkladu a ze
vzorce pro vychází ze
zapojení naprázdno, tak jak znázorňuje první obrázek tohoto příkladu a ze
vzorce pro 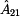 . .
Z výpočtu prvku 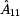 víme, že výstupní
napětí je rovno víme, že výstupní
napětí je rovno
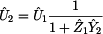
Z obrázku lze snadno odvodit i vztah pro proud 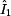 : :
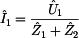
Tyto poznatky nám plně dostačují pro výpočet prvku
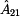 : :
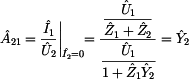
Výpočet prvku 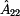 je založen na
zapojení naktrátko podle druhého obrázku tohoto příkladu a ze vzorce pro je založen na
zapojení naktrátko podle druhého obrázku tohoto příkladu a ze vzorce pro
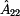 . .
Tak jako u prvku 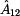 zde platí rovnost obou proudů zde platí rovnost obou proudů 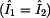 . Explicitní
vyjádření zde není nutné, neboť se navzájem ve vzorci vykrátí. . Explicitní
vyjádření zde není nutné, neboť se navzájem ve vzorci vykrátí.
Dosazením do vzorce dostáváme prvek 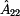 : :
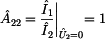
Vyjádřením všech prvků jsme obdrželi výslednou
kaskádní matici (A), která je rovna:
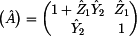
Jelikož v tomto případě naplatí rovnost prvků
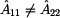 ,
nejedná se v tomto případě o podélně souměřný dvoubran. ,
nejedná se v tomto případě o podélně souměřný dvoubran.
Výpočtem determinantu kaskádní matice |A| si ověříme
reciprocitu dvoubranu.
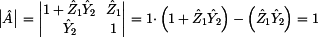
Z rovnosti opět vyplývá reciprocita
dvoubranu. |
Příklad 4: Dvoubran typu "T-článek"
| Příklad. |
Výpočet jednoduchého dvojbranu typu "T-článek":
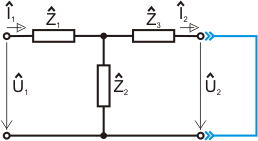
Mějme dvojbran (T-článek) definovaný na následujícím
obrázku:
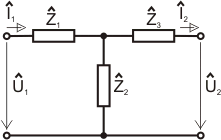
Prvek 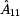 spočteme ze zapojení naprázdno dle prvního obrázku tohoto příkladu a ze
vztahu pro prvek
spočteme ze zapojení naprázdno dle prvního obrázku tohoto příkladu a ze
vztahu pro prvek 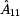 . .
Je-li výstupní proud 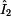 nulový, potom
impedance nulový, potom
impedance 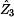 nemá na obvod žádný vliv a jedná se tedy opět o nezatížený
odporový dělič. Vztah pro výstupní napětí, jsme si již odvodili v
příkladě č.:3 a je rovno: nemá na obvod žádný vliv a jedná se tedy opět o nezatížený
odporový dělič. Vztah pro výstupní napětí, jsme si již odvodili v
příkladě č.:3 a je rovno:
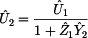
Nyní již stačí dosadit do vzorce, a dostaneme
tím tak prvek 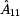 : :
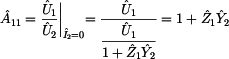
Nyní
přistoupíme k výpočtu prvku 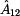 , který vychází ze
zapojení nakrátko (viz. druhý obrázek tohoto příkladu) a ze vzorce pro , který vychází ze
zapojení nakrátko (viz. druhý obrázek tohoto příkladu) a ze vzorce pro
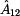 a jeví se na výpočet jako nejtěžší.
a jeví se na výpočet jako nejtěžší.
Nejprve si vyjádříme napětí 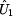 : :
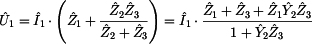
Nyní si potřebujeme vyjádřit proud 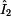 ,
který získáme z rovnic pro rovnosti úbytku napětí na impedancích ,
který získáme z rovnic pro rovnosti úbytku napětí na impedancích 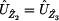
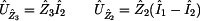
Položíme-li tyto výrazy do rovnosti, dostaneme
rovnici pro 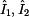 : :
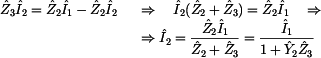
Dosazením získaných mezivýsledků do vzorce
získáme prvek 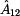 : :
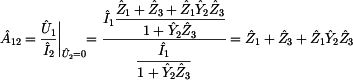
Prvek 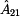 získáme ze
zapojení naprázdno a ze vztahu pro získáme ze
zapojení naprázdno a ze vztahu pro 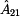 . .
Vyjdeme opět
z prvního obráyku tohoto příkladu. Jelikož výstupní proud 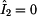 , nemá
impedance , nemá
impedance 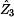 v obvodu žádný význam. Jedná se tedy opět o nezatížený odporový
dělič. v obvodu žádný význam. Jedná se tedy opět o nezatížený odporový
dělič.
Vajádříme si vstupní proud dvojranu 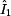 : :
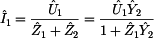
Náslědně si vyjádříme i výstupní napětí dvojbranu,
které ale už dobře všichni známe:
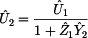
Vyjádřené hodnoty vstupního proudu 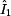 a
výstupního napětí dvojbranu a
výstupního napětí dvojbranu 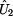 dosadíme do vzorce
a získáme tak prvek dosadíme do vzorce
a získáme tak prvek 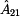 : :
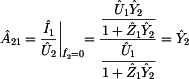
Poslední zbývající prvek 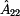 vyjádříme ze
zapojení nakrátko dle druhého obrázku tohoto příkladu a ze vztahu pro vyjádříme ze
zapojení nakrátko dle druhého obrázku tohoto příkladu a ze vztahu pro 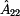 . .
Vyjdeme z úvah, které jsem použili pro výpočet prvku 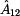 . Nyní nám ale bude
stačit rovnice rovnosti proudů a z ní vyjádřený výstupní proud . Nyní nám ale bude
stačit rovnice rovnosti proudů a z ní vyjádřený výstupní proud 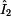 : :
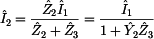
Takto vyjádřený výstupní proud nám stačí jenom
dosadit do vztahu, čímž dostaneme pro parametr 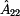 vztah: vztah:
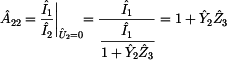
Nyní, když máme vyjádřeny všechny prvky, je
kaskádní matice (A) rovna:
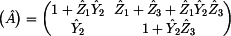
Výpočtem determinantu kaskádní matice
|A| si ověříme reciprocitu dvoubranu.
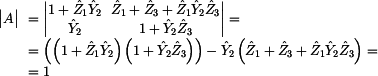
Z rovnosti determinantu vyplývá
reciprocita dvoubranu.
Z nerovnosti parametrů 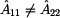 můžeme usoudit, že
se nejedná o podélně souměrný dvoubran. můžeme usoudit, že
se nejedná o podélně souměrný dvoubran.
|
Neřešené příklady
Příklad 1: Dvoubran typu "velké Gamma"
| Příklad. |
Dvoubran typu "velké Gamma":
Mějme dvojbran
definovaný na následujícím obrázku:
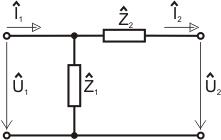
Úkol:
Spočtěte kaskádní matici dvojbranu, jednak přímo, jednak pomocí
dílčích dvojbranů.
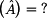
|
Příklad 2: Dvoubran typu "Pí-článek"
| Příklad. |
Dvoubran typu " -článek": -článek":
Mějme dvojbran definovaný na následujícím obrázku:
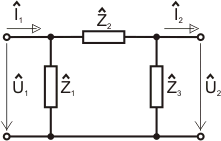
Úkol a)
Spočtěte kaskádní matici dvojbranu.
Úkol b) Na
základě spočtené kaskádní matice současně ověřte i platnost vzorce
pro kaskádní spojení dvojbranů vhodným spojením dvojbranů řešených
v příkladech 1..4
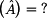
|
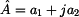
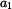 je reálná a
je reálná a 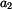 imaginární
složka,
imaginární
složka, 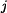 je imaginární jednotka s touto vyjímečnou vlastností
je imaginární jednotka s touto vyjímečnou vlastností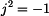
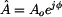
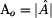 je
absolutní hodnota nebo modul a
je
absolutní hodnota nebo modul a 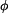 je úhel, který s osou X
svírá přímka směřující z počátku do komplexního čísla, viz část Geometrické
znázornění komplexních čísel. V analytické geometrii se jedná o průvodič bodu. V
teorii obvodů budeme však často mluvit o amplitudě
je úhel, který s osou X
svírá přímka směřující z počátku do komplexního čísla, viz část Geometrické
znázornění komplexních čísel. V analytické geometrii se jedná o průvodič bodu. V
teorii obvodů budeme však často mluvit o amplitudě 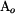 a fázovém úhlu, či
jednoduše jen fázi
a fázovém úhlu, či
jednoduše jen fázi 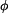 .
.

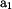 a imaginární složka
a imaginární složka 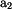 jsou jeho kartézskými souřadnicemi, zatímco amplituda
jsou jeho kartézskými souřadnicemi, zatímco amplituda
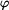 souřadnicemi polárními, po řadě průvodič a úhel.
souřadnicemi polárními, po řadě průvodič a úhel. 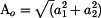 ......
...... 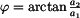
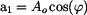 ......
...... 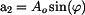
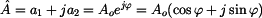
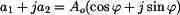
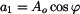 .....
..... 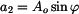
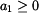 , tj. pro fázový úhel v
rozsahu
, tj. pro fázový úhel v
rozsahu 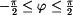 . Pokud je reálná složka záporná,
. Pokud je reálná složka záporná, 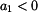 , je fázový úhel v
dalších dvou kvadrantech. V tomto případě je nutno použít vztahů
, je fázový úhel v
dalších dvou kvadrantech. V tomto případě je nutno použít vztahů  pro
pro 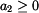
 pro
pro 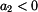
 nebo ve stupních
nebo ve stupních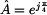
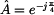
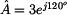
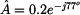
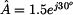
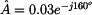
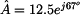
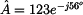
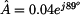
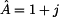
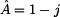
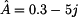
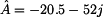
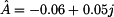
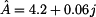
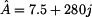
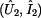 . Závislými
proměnnými jsou pak proměnné
. Závislými
proměnnými jsou pak proměnné 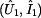 .
.

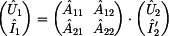
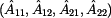 a se dvěma nezávislými veličinami
a se dvěma nezávislými veličinami 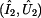
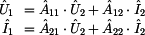
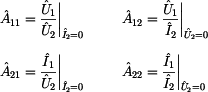

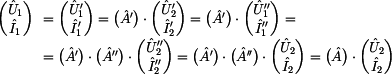
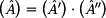

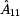 je
definován jako poměr vstupního napětí ku výstupnímu při zapojení
výstupních svorek dvojbranu naprázdno, tak jak ukazuje předchozí obrázek.
je
definován jako poměr vstupního napětí ku výstupnímu při zapojení
výstupních svorek dvojbranu naprázdno, tak jak ukazuje předchozí obrázek.
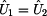 ),
čili prvek
),
čili prvek 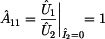

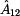 je
definovaný jako poměr vstupního napětí ku výstupnímu proudu při zapojení
výstupních svorek dvojbranu nakrátko, tak jak je znázorněno na předchozím
obrázku.
je
definovaný jako poměr vstupního napětí ku výstupnímu proudu při zapojení
výstupních svorek dvojbranu nakrátko, tak jak je znázorněno na předchozím
obrázku. 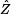 je zkratována a
nemá tedy v obvodu žádný význam. Z toho můžeme odvodit, že platí
je zkratována a
nemá tedy v obvodu žádný význam. Z toho můžeme odvodit, že platí 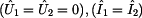 . Při
znalosti těchto poměrů lze již snadno vypočítat prvek
. Při
znalosti těchto poměrů lze již snadno vypočítat prvek 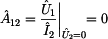
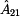 . K analýze použijeme tedy prvně uvedený obrázek z tohoto
příkladu.
. K analýze použijeme tedy prvně uvedený obrázek z tohoto
příkladu. 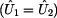 , viz obrázek. Vstupní proud dvojbranu
, viz obrázek. Vstupní proud dvojbranu  snadno vyjádříme
snadno vyjádříme
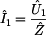 .
Nyní již známe vše co potřebujeme pro výpočet prvku
.
Nyní již známe vše co potřebujeme pro výpočet prvku 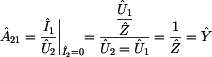
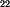 je definován jako
poměr vstupního ku výstupnímu proudu při zapojení výstupních svorek
dvojbranu nakrátko, viz. druhý obrázek tohoto příkladu.
je definován jako
poměr vstupního ku výstupnímu proudu při zapojení výstupních svorek
dvojbranu nakrátko, viz. druhý obrázek tohoto příkladu. 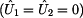 a i rovnost vstupního a výstupního proudu
a i rovnost vstupního a výstupního proudu 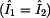 , neboť impedance
, neboť impedance
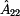
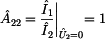
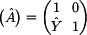
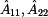 si snadno oběříme
souměrnost dvojbranu. Jelikož v našem případě platí
si snadno oběříme
souměrnost dvojbranu. Jelikož v našem případě platí 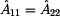 ,
můžeme řící, že dvojbran je podélně souměrný.
,
můžeme řící, že dvojbran je podélně souměrný. 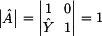

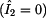 bude zřejmě nulový i proud
bude zřejmě nulový i proud 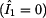 , neboť na
impedanci
, neboť na
impedanci 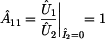

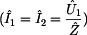 . Napětí tentokrát
vyjadřovat nemusíme, neboť si plně vystačíme s proudy. Dosazením
předchozích úvah do vzorce pro prvek
. Napětí tentokrát
vyjadřovat nemusíme, neboť si plně vystačíme s proudy. Dosazením
předchozích úvah do vzorce pro prvek 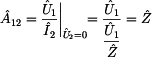
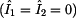 , neboť nedochází k
úbytku napětí na impedanci
, neboť nedochází k
úbytku napětí na impedanci 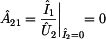
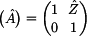
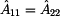 můžeme
konstatovat, že se jedná o podélně souměrný dvoubran. Výpočtem
determinantu kaskádní matice |A| si opět ověříme
reciprocitu dvoubranu.
můžeme
konstatovat, že se jedná o podélně souměrný dvoubran. Výpočtem
determinantu kaskádní matice |A| si opět ověříme
reciprocitu dvoubranu. 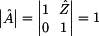

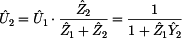
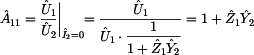

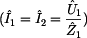 .
. 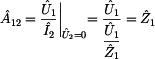
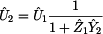
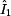 :
: 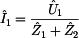
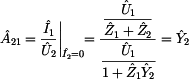
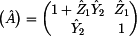
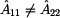 ,
nejedná se v tomto případě o podélně souměřný dvoubran.
,
nejedná se v tomto případě o podélně souměřný dvoubran.
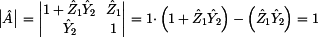

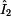 nulový, potom
impedance
nulový, potom
impedance 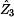 nemá na obvod žádný vliv a jedná se tedy opět o nezatížený
odporový dělič. Vztah pro výstupní napětí, jsme si již odvodili v
příkladě č.:3 a je rovno:
nemá na obvod žádný vliv a jedná se tedy opět o nezatížený
odporový dělič. Vztah pro výstupní napětí, jsme si již odvodili v
příkladě č.:3 a je rovno: 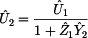
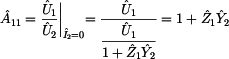

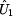 :
:
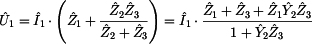
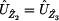
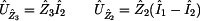
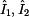 :
: 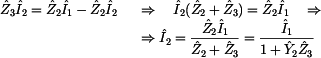
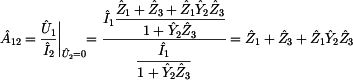
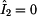 , nemá
impedance
, nemá
impedance 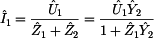
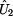 dosadíme do vzorce
a získáme tak prvek
dosadíme do vzorce
a získáme tak prvek